L’affidabilità di un test diagnostico: matematica e teorema di Bayes
Se un individuo risulta positivo a un test diagnostico, qual è la probabilità che sia effettivamente malato? In altri termini, quanto è affidabile il risultato del test? La risposta a questa domanda non è banale come potrebbe sembrare.
Cerchiamo quindi di formalizzare il problema, vedendo una semplice applicazione del teorema di Bayes per approfondire il significato di affidabilità di un test diagnostico, e approfittandone per dare qualche definizione in più riguardo ai test diagnostici in generale.
Iniziamo con un quesito:
Nel paese di Biribò il dott. Osvaldo sospetta che il proprio paziente Gesualdo abbia una certa malattia. Per validare la sua ipotesi, il dottore sottopone Gesualdo a un test diagnostico efficace al 99%, cioè in grado di rilevare la presenza (o l’assenza) della malattia nel 99% dei casi.
Sapendo che solo l’1% degli abitanti del paese di Biribò hanno quella determinata malattia, qual è la probabilità che, se il test dovesse dare esito positivo, Gesualdo sia effettivamente malato?
Probabilmente rispondereste che la probabilità è del 99%. Tuttavia, la risposta corretta, e forse un po’ controintuitiva, è 50%.
Vediamo il perché con un esempio numerico.
Supponiamo che nel paese di Biribò ci siano 10000 abitanti. Il numero di persone malate è quindi 100, ovvero l’1% di 10000, e il numero di persone sane è 9900.
Sottoponiamo tutti gli abitanti al test. Il test darà esito positivo, e quindi corretto, su 99 malati, e negativo su 1 malato (falso negativo). Il test darà poi esito positivo su 99 persone sane (falsi positivi), e negativo sulle restanti.
Abbiamo quindi lo stesso identico numero di persone sane e malate su cui il test ha dato esito positivo! Se scegliamo a caso una delle persone positive al test abbiamo quindi il 50% di possibilità che sia effettivamente malata.
Ho volutamente preso questo esempio, costruito in modo un po’ vago, per arrivare a fare alcune riflessioni: innanzitutto, prima di dare risposte affrettate, è necessario conoscere bene tutti gli elementi che costituiscono il problema e, soprattutto, aver ben chiare le definizioni, altrimenti il rischio di venire ingannati è molto elevato (in questo quesito, ad esempio, non ho specificato con sufficiente chiarezza il significato di efficacia di un test). Un’altra questione, più tecnica, che salta all’occhio, è che la risposta del quesito dipende non solo dall’efficacia del test, ma anche da quanto è diffusa la malattia nella popolazione.
Cerchiamo quindi di fare un po’ d’ordine dando qualche definizione in più.
Come si valuta l’affidabilità di un test diagnostico?
Tabella di errata classificazione, falsi positivi, falsi negativi.
Supponiamo di avere a disposizione un test diagnostico per una certa malattia. Come possiamo validarlo? Ovvero, come possiamo sapere se il test è accurato oppure no? Una possibile modalità di validazione del test è quella di fare uno studio statistico conoscendo a priori la corretta classificazione del gruppo di pazienti che sottoporremo al test. In altre parole, dato un gruppo di pazienti, dovremmo conoscere a priori quanti sono malati e quanti sono sani, sottoporli al test, e contare quanti vengono correttamente individuati. In sostanza, il test dovrebbe essere comparato con un altro metodo di classificazione, assunto come riferimento, che viene chiamato gold standard (non sempre il gold standard è risultato di un test diagnostico, ma potrebbe essere costituito anche da evidenze biologiche).
Uno studio statistico per la validazione di un test è basato sulla tabella di errata classificazione (o matrice di confusione) che contiene il numero di casi classificati correttamente o falsamente.
Sulla diagonale principale abbiamo due classificazioni corrette: veri positivi (VP, pazienti malati individuati dal test) e veri negativi (VN, pazienti sani classificati correttamente). Sulla diagonale secondaria abbiamo invece due classificazioni non corrette: falsi positivi (FP, pazienti sani classificati come malati) e falsi negativi (FN, pazienti malati classificati come sani).
Il test perfetto, che purtroppo non esiste, non dovrebbe produrre né falsi positivi né falsi negativi.
Accuratezza, sensibilità e specificità caratterizzano l’affidabilità di un test diagnostico.
Diamo ora tre definizioni molto importanti per misurare l’affidabilità di un test diagnostico: accuratezza, sensibilità e specificità.
- ACCURATEZZA = (VP+VN)/TOT PAZIENTI¹. L’accuratezza misura quindi la percentuale di diagnosi corrette, ovvero quanti pazienti vengono classificati correttamente.
- SENSIBILITÀ = VP/TOT MALATI¹. La sensibilità è la proporzione di malati che vengono classificati in maniera corretta. Se il test è molto sensibile riuscirà a individuare, per fare un esempio, anche basse concentrazioni di virus, dando meno risultati falsi negativi. In altri termini, la sensibilità è la probabilità che un individuo malato risulti positivo al test, P(+|M)².
Un test è sensibile al 100% quando tutti i malati risultano positivi, quindi nessun malato sfuggirà al test. - SPECIFICITÀ = VN/TOT SANI¹. La specificità è la proporzione di sani classificati correttamente. Un test altamente specifico riesce a non confondere il vero obiettivo, ad esempio il virus, con altre forme simili, e darà quindi meno esiti falsi positivi. In altri termini, la specificità è la probabilità che un individuo sano risulti negativo al test, P(-|S)².
Un test è specifico al 100% quando tutti i sani risultano negativi, quindi nessun paziente sano avrà una diagnosi errata.
In genere è difficile ottenere un test che sia altamente specifico e al contempo sensibile: rendere un test più specifico può renderlo meno sensibile, e viceversa. Quindi la scelta di un test dipende essenzialmente da ciò che stiamo cercando: se il fine è l’individuazione del maggior numero di malati il test migliore è quello con sensibilità più elevata. Se il fine è fare una diagnosi accurata allora è meglio un test con specificità elevata. A questo, per chi volesse approfondire, ricordiamo che la sensibilità e la specificità di un test possono essere messe in relazione tramite la curva ROC (Receiver Operating Characteristic).
Perché anche i test più efficaci possono fallire?
Applicazione del teorema di Bayes: valore predittivo di un test diagnostico
Ora abbiamo definito accuratezza, sensibilità e specificità del nostro test, ma questi elementi non ci permettono ancora di rispondere immediatamente alla domanda, di fondamentale interesse nella pratica clinica: se un paziente risulta positivo al test, qual è la probabilità che egli sia effettivamente malato? (questa probabilità è anche chiamata valore predittivo positivo del test)
La specificità e la sensibilità infatti corrispondono alla probabilità che il test sia positivo o negativo in pazienti di cui conosciamo già lo stato di salute. Quello che ci interessa ora è esattamente il contrario: sapendo il risultato del test, vogliamo conoscere lo stato di salute del paziente.
In termini probabilistici: noi conosciamo P(+|M), la sensibilità, e vogliamo trovare P(M|+), il valore predittivo del test. Con P(M) indichiamo la prevalenza della malattia, ovvero quanto è diffusa la malattia nella popolazione, con P(S) la probabilità di essere sani, con P(+) la probabilità che il test risulti positivo, e applichiamo il teorema di Bayes³:
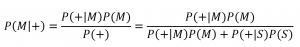
Abbiamo dunque appena trovato il valore predittivo positivo del test, VPP. In letteratura si trova infatti spesso la seguente formula, che è la stessa che abbiamo appena scritto con “etichette” più eloquenti, ma senza spiegazioni circa la sua origine:
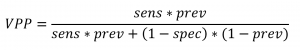
Tornando al quesito iniziale, adesso dovrebbe essere chiaro che per rispondere alla domanda bisogna calcolare il valore predittivo del test, dove la specificità e la sensibilità sono entrambe del 99% e la prevalenza della malattia è dell’1%:
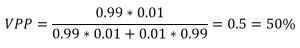
Il valore predittivo è del 50%, come avevamo trovato!
Il risultato, tuttavia, è piuttosto scadente. Nonostante il test abbia sensibilità e specificità elevate, la probabilità che un individuo positivo sia malato non è soddisfacente, perché questo valore dipende in larga misura anche da quanto è diffusa la malattia nella popolazione.
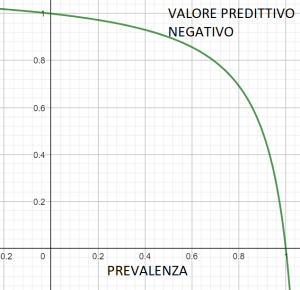
Per visualizzare quanto il valore predittivo positivo dipenda dalla prevalenza potremmo disegnare un grafico, ristretto a valori tra 0 e 1.
Date specificità e sensibilità, è abbastanza evidente che il grafico del VPP sia qualcosa di questo tipo.
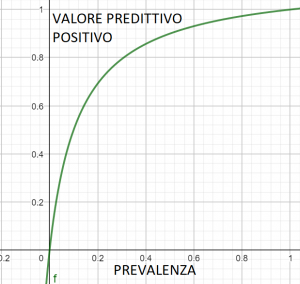
Il valore predittivo positivo cresce dunque al crescere della prevalenza. Più la prevalenza della malattia si avvicina al 100% più il valore predittivo positivo è elevato. Ma, visto che la prevalenza della malattia non è manipolabile a priori, come possiamo ottenere un valore predittivo migliore? Per rispondere a questa domanda si potrebbe procedere in due modi: o si utilizza un test con performance migliori, o si ripete il test più volte.
Proseguiamo dunque vedendo un esempio pratico e attuale di come aumenta il valore predittivo di un test ripetendolo più volte.
Perché fare due tamponi per capire se si è guariti dal Coronavirus?
Fino a non molto tempo fa, per essere sicuri che un paziente affetto da COVID-19 fosse guarito, si effettuavano 2 tamponi a distanza di 24 ore l’uno dall’altro. Se l’esito di entrambi era negativo allora si poteva affermare con una certa sicurezza che il paziente fosse guarito.
Supponiamo che il test diagnostico utilizzato abbia specificità e sensibilità del 95% e calcoliamo, contrariamente a quanto fatto prima, P(S|-), il valore predittivo negativo del test, assumendo una prevalenza del 25%.
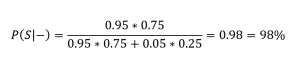
Quindi il paziente ha probabilità del 98% di essere guarito. Ripetiamo ora il test, applicando di nuovo il teorema di Bayes, aggiornando opportunamente la probabilità che il paziente sia sano.
La probabilità è salita ben al 99,8%!
Inoltre, come possiamo intuire, il valore predittivo negativo in funzione della prevalenza è decrescente, quindi meno è diffusa la malattia più il valore predittivo si avvicina al 100%.
Per completezza, riportiamo per il valore predittivo negativo calcoli analoghi a quelli fatti per il valore predittivo positivo.
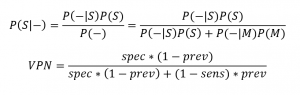
In conclusione, avendo ora qualche strumento in più per comprendere il valore dei dati di un test diagnostico e per capire quando un risultato può considerarsi affidabile, senza incappare in errori grossolani, potremmo provare a risolvere il problema del dott. Osvaldo, non soddisfatto del risultato del test, rispondendo al quesito:
E se il dott. Osvaldo ripetesse il test su Gesualdo, di quanto aumenterebbe la probabilità che Gesualdo sia effettivamente malato se anche il secondo test risultasse positivo?
Note:
- TOT PAZIENTI = VP + VN + FP + FN, TOT MALATI = VP + FN, TOT SANI = FP + VN
- P(+|M) e P(-|S) sono, rispettivamente, le probabilità che il test risulti positivo sapendo che il paziente è malato (sensibilità), e che il test risulti negativo sapendo che paziente è sano (specificità). Si tratta di probabilità condizionate perché sappiamo che l’evento a destra della barretta verticale si è verificato.
- Teorema di Bayes:
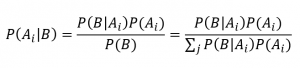dove Aj partizionano lo spazio degli eventi.
Il teorema può essere anche scritto nella forma seguente, dove A e il suo complementare costituiscono per costruzione una partizione: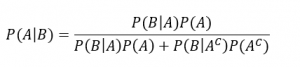
Nel nostro caso useremo la partizione data da M e S: nella popolazione gli individui sono sani oppure sono malati, l’intersezione è chiaramente vuota (non ci sono individui contemporaneamente sani e malati). Quindi S è il complementare di M.
Fonti:
Introductory Biostatistics, 2nd Edition, Chap T. Le, Lynn E. Eberly
- Probabilità, Caravenna F., Dai Pra P.
