Esercizi sui test diagnostici: sensibilità, specificità, valore predittivo, curva ROC

ESERCIZI SUI TEST DIAGNOSTICI

In questa pagina riportiamo alcuni esercizi sui test diagnostici, focalizzandoci in particolare sul calcolo di sensibilità, specificità e valore predittivo e sulla costruzione di una curva ROC.
Alcuni testi di questi esercizi si trovano in Pagano, Gauvreau (1) o Daniel, Cross (2), che consigliamo di consultare per esercizi aggiuntivi sui test diagnostici, mentre altri sono di nostra invenzione. 

DEFINIZIONI E FORMULE UTILI PER RISOLVERE GLI ESERCIZI SUI TEST DIAGNOSTICI

Riprendiamo, per praticità, qualche concetto e definizione di base.

Per un approfondimento rimandiamo agli articoli dedicati, che lasciamo in link.

  • SENSIBILITÀ: probabilità che il test dia un risultato positivo se un individuo è malato. SENSIBILITÀ = VERI POSITIVI/TOT MALATI 
  • SPECIFICITÀ: probabilità che il test dia un risultato negativo se un individuo è sano. SPECIFICITÀ = VERI NEGATIVI/TOT SANI
  • VALORE PREDITTIVO POSITIVO: probabilità che un individuo che risulta positivo a un test sia realmente malato. \small VPP \large= \frac{sens\cdot prev}{sens\cdot prev+(1-spec)\cdot(1-prev)}
  • VALORE PREDITTIVO NEGATIVO: probabilità che un individuo che risulta negativo a un test sia realmente sano. \small VPN \large= \frac{spec\cdot (1-prev)}{spec\cdot (1-prev)+(1-sens)\cdot prev}

ESERCIZIO 1: sensibilità, specificità, falso positivo, falso negativo, valore predittivo

Uno studio ha affermato che la sensibilità della mammografia quale test di screening per l’individuazione del cancro della mammella è 0,85; la sua specificità è 0,80.

  1. Qual è la probabilità di un falso negativo?
  2. Qual è la probabilità di un falso positivo?
  3. In una popolazione in cui la probabilità che una donna abbia un cancro della mammella è 0,0025, qual è la probabilità che una donna abbia un cancro in presenza di una mammografia positiva?

SOLUZIONE ESERCIZIO 1

  1. Un falso negativo si verifica quando il test dà un esito negativo su un paziente che in realtà è malato. La sensibilità di un test corrisponde alla probabilità di ottenere un test positivo su un paziente malato, pertanto la probabilità di un falso negativo (evento complementare) è 1 – sensibilità, cioè 0,15.
    Infatti, se il test ha una sensibilità pari a 0,85, significa che se sottoponiamo al test 100 malati 85 di essi saranno veri positivi, mentre 15 saranno falsi negativi.
  2. Un falso positivo si verifica quando il test dà un esito positivo su un paziente che in realtà è sano. La specificità di un test corrisponde alla probabilità di ottenere un test negativo su un paziente sano, pertanto la probabilità di un falso positivo (evento complementare) è 1 – specificità, cioè 0,20. Infatti, se il test ha una specificità pari a 0,80, significa che se sottoponiamo al test 100 pazienti sani 80 di essi saranno veri negativi, mentre 15 saranno falsi positivi.
  3. Per rispondere a questa domanda bisogna calcolare il valore predittivo positivo del test, sapendo che la prevalenza della malattia è 0,0025.


    \small VPP \large= \frac{sens\cdot prev}{sens\cdot prev+(1-spec)\cdot(1-prev)}=\frac{0,85\cdot 0,0025}{0,85\cdot 0,0025+(1-0,80)\cdot(1-0,0025)}= \frac{0,002125}{0,002125+0,20\cdot 0,9975}=\small 0,011


    Questo significa che, se una donna scelta a caso nella popolazione ha una probabilità dello 0,25% di avere il cancro alla mammella (probabilità a priori), a seguito di mammografia positiva questa probabilità sale all’1,1% (probabilità a posteriori), ed è quindi aumentata di 4,4 volte.

    banner acqua idrogenata desktop

ESERCIZIO 2: sensibilità, specificità, valore predittivo

I dati di seguito riportati sono estratti da uno studio che esamina l’uso della ventricolografia radionuclidica quale test diagnostico per l’individuazione della patologia coronarica.

tabella esercizi test diagnostici sensibilità, specificità, valore predittivo
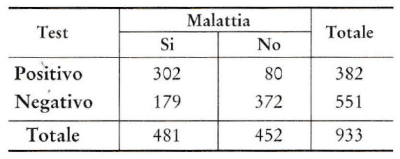
  1. Qual è la sensibilità della ventricolografia radionuclidica in questo studio? Qual è la specificità?
  2. Per una popolazione in cui la probabilità di presentare patologie coronariche è 0,10, calcolare la probabilità che un soggetto presenti la malattia in presenza di un risultato positivo alla ventricolografia radionuclidica.
  3. Qual è il valore predittivo di un test negativo?

SOLUZIONE ESERCIZIO 2

  1. La sensibilità si trova calcolando il rapporto tra i veri positivi e il totale dei malati: SENSIBILITÀ = VERI POSITIVI/TOT MALATI = 302/481 = 0,63.
    La specificità si trova calcolando il rapporto tra i veri negativi e il totale dei sani: SPECIFICITÀ = VERI NEGATIVI/TOT SANI = 372/452 = 0,82.
  2. Dobbiamo calcolare il valore predittivo positivo del test, sapendo che la prevalenza della malattia è 0,10.


    \small VPP \large= \frac{sens\cdot prev}{sens\cdot prev+(1-spec)\cdot(1-prev)}=\frac{0,63\cdot 0,10}{0,63\cdot 0,10+(1-0,82)\cdot(1-0,10)}= \frac{0,063}{0,063+0,18\cdot 0,90}=\small 0,28

    Questo significa che, se un individuo scelto a caso nella popolazione ha una probabilità del 10% di avere patologie coronariche (probabilità a priori), a seguito di ventricolografia radionuclidica positiva questa probabilità sale al 28% (probabilità a posteriori), ed è quindi aumentata di quasi 3 volte.

  3. Calcoliamo ora il valore predittivo negativo del test.


    \small VPN \large= \frac{spec\cdot (1-prev)}{spec\cdot (1-prev)+(1-sens)\cdot prev}=\frac{0,82\cdot 0,90}{0,82\cdot 0,90+0,37\cdot 0,10}= \frac{0,738}{0,738+0,037}=\small 0,95

ESERCIZIO 3: curva ROC e cut-off ottimo

Supponiamo che i dati di uno studio siano quelli riportati nella tabella seguente.

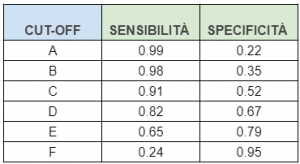
tabella esercizi test diagnostici curva roc

Si costruisca la curva ROC del test e si determini il cut-off ottimale utilizzando l’indice di Youden.

SOLUZIONE ESERCIZIO 3

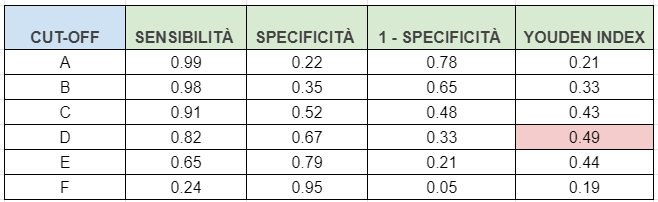
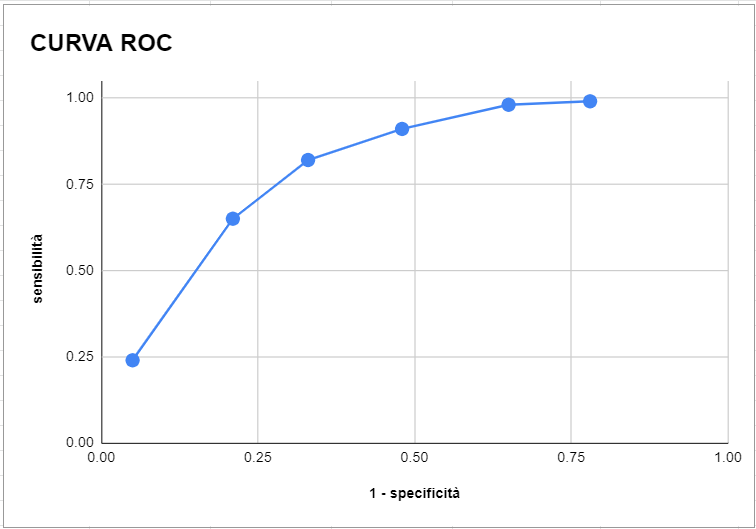
Per poter disegnare la curva ROC è necessario calcolare, per ogni valore di cut-off, 1 – specificità. Per ogni cut-off, il corrispondente punto della della curva ROC avrà come coordinata orizzontale 1 – specificità e come coordinata verticale la sensibilità.

Per trovare invece cut-off ottimale calcoliamo, per ogni valore di cut-off, sensibilità + specificità – 1. L’indice di Youden  J = maxc {sensibilità(c) + specificità(c) − 1} è il massimo tra questi valori, che si ottiene in corrispondenza del cut-off C.

tabella esercizio curva roc youden index
plot curva roc esercizio

ESERCIZIO 4: sensibilità, specificità, falso positivo, falso negativo, valore predittivo

Un team di ricercatori vorrebbe capire se un certo sintomo possa essere utile nella diagnosi di una certa malattia. In un campione di 775 pazienti con la malattia, 744 hanno riferito di avere il sintomo. In un altro campione di 1380 soggetti senza la malattia, 21 hanno riferito di avere il sintomo.

  1. In questo contesto, che cos’è un falso positivo?
  2. Cos’è un falso negativo?
  3. Si calcoli la sensibilità del sintomo.
  4. Si calcoli la specificità del sintomo.
  5. Se la prevalenza della malattia nella popolazione è 0,001, qual è il valore predittivo positivo del sintomo?
  6. Qual è il valore predittivo negativo del sintomo?
  7. Si trovino i valori predittivi positivi e negativi del sintomo nei casi in cui la prevalenza sia:
    1. 0,0001
    2. 0,01
    3. 0,1
  8. Facendo riferimento ai valori appena trovati, che conclusioni si possono trarre riguardo al valore predittivo del sintomo?

SOLUZIONE ESERCIZIO 4

  1. In questo contesto un falso positivo è un soggetto che ha il sintomo ma non è malato.
  2. Un falso negativo è un soggetto che non ha il sintomo ma è malato.
  3. Per determinare la sensibilità, calcoliamo il rapporto tra il numero delle persone che hanno il sintomo e sono malate (veri positivi) e il totale delle persone malate: SENSIBILITÀ = VERI POSITIVI/TOT MALATI = 744/775 = 0,96
  4. Per determinare la specificità, calcoliamo il rapporto tra il numero delle persone che non hanno il sintomo e sono sane (veri negativi, 1380-21=1359) e il totale delle persone sane: SPECIFICITÀ = VERI NEGATIVI/TOT SANI = 1359/1380 = 0,98
  5. prev = 0,001

    \small VPP \large= \frac{sens\cdot prev}{sens\cdot prev+(1-spec)\cdot(1-prev)}=\frac{0,96\cdot 0,001}{0,96\cdot 0,001+(1-0,98)\cdot(1-0,001)}= \frac{0,00096}{0,00096+0,02\cdot 0,999}=\small 0,045

  6. prev = 0,001

    \small VPN \large= \frac{spec\cdot (1-prev)}{spec\cdot (1-prev)+(1-sens)\cdot prev}=\frac{0,98\cdot 0,999}{0,98\cdot 0,999+0,04\cdot 0,001}= \frac{0,979}{0,979+0,00004}=\small 0,9999591

  7. Calcoliamo i valori predittivi al variare della prevalenza.
    1. prev = 0,0001


      \small VPP \large= \frac{sens\cdot prev}{sens\cdot prev+(1-spec)\cdot(1-prev)}=\frac{0,96\cdot 0,0001}{0,96\cdot 0,0001+(1-0,98)\cdot(1-0,0001)}= \frac{0,000096}{0,000096+0,02\cdot 0,9999}=\small 0,0048

      \small VPN \large= \frac{spec\cdot (1-prev)}{spec\cdot (1-prev)+(1-sens)\cdot prev}=\frac{0,98\cdot 0,9999}{0,98\cdot 0,9999+0,04\cdot 0,0001}= \frac{0,9799}{0,9799+0,000004}=\small 0,99999591

    2. prev = 0,01


      \small VPP \large= \frac{sens\cdot prev}{sens\cdot prev+(1-spec)\cdot(1-prev)}=\frac{0,96\cdot 0,01}{0,96\cdot 0,01+(1-0,98)\cdot(1-0,01)}= \frac{0,0096}{0,0096+0,02\cdot 0,99}=\small 0,327

      \small VPN \large= \frac{spec\cdot (1-prev)}{spec\cdot (1-prev)+(1-sens)\cdot prev}=\frac{0,98\cdot 0,99}{0,98\cdot 0,99+0,04\cdot 0,01}= \frac{0,9702}{0,9702+0,0004}=\small 0,99959

    3. prev = 0,1


      \small VPP \large= \frac{sens\cdot prev}{sens\cdot prev+(1-spec)\cdot(1-prev)}=\frac{0,96\cdot 0,1}{0,96\cdot 0,1+(1-0,98)\cdot(1-0,1)}= \frac{0,096}{0,096+0,02\cdot 0,9}=\small 0,839

      \small VPN \large= \frac{spec\cdot (1-prev)}{spec\cdot (1-prev)+(1-sens)\cdot prev}=\frac{0,98\cdot 0,9}{0,98\cdot 0,9+0,04\cdot 0,1}= \frac{0,882}{0,882+0,004}=\small 0,995

  8. Se la prevalenza della malattia è molto bassa, il valore predittivo positivo del test è poco rilevante. Infatti, se la prevalenza è 0,0001 allora VPP = 0,48% (ovvero se una persona presenta il sintomo ha una probabilità dello 0,48% di avere realmente la malattia). Se la prevalenza è 0,001 allora VPP = 4,5%
    Mentre per valori della prevalenza più elevati il valore predittivo del test è più alto. Infatti, se la prevalenza è 0,01 allora VPP = 32,7%, se la prevalenza è 0,1 allora VPP = 84% 
    Il valore predittivo negativo del sintomo, invece, per ogni valore della prevalenza che abbiamo considerato, è sempre molto alto.

 

Samanta Zagani

Fonti e note:

  • (1) Biostatistica, Marcello Pagano, Kimberlee Gauvreau
  • (2) Biostatistics: A Foundation for Analysis in the Health Sciences, Daniel, Wayne W., Cross, Chad L.
  • Introductory Biostatistics, 2nd Edition, Chap T. Le, Lynn E. Eberly

Per approfondire:

I test diagnostici: la terza tappa verso la diagnosi

Affidabilità di un test diagnostico: matematica e teorema di Bayes

Esami diagnostici per immagini

L’anamnesi medica: l’inizio della diagnosi

L’Esame Obiettivo: la seconda tappa verso la diagnosi