Likelihood Ratio (Rapporto di verosimiglianza) e Nomogramma di Fagan
LIKELIHOOD RATIO (RAPPORTO DI VEROSIMIGLIANZA) E NOMOGRAMMA DI FAGAN
Il rapporto di verosimiglianza, o likelihood ratio, di un test è un parametro che, oltre a essere un indicatore dell’accuratezza del test, viene utilizzato per determinare la probabilità che un individuo abbia, o meno, una certa malattia.
Sappiamo che la procedura per ottenere la diagnosi di una malattia è costituita da una sequenza di indagini:
- durante l’anamnesi e l’esame obiettivo il medico raccoglie informazioni (sintomi, fattori di rischio, segni, prevalenza della malattia, ecc.) che gli consentono di formulare una ipotesi diagnostica che avrà una certa probabilità → probabilità pre-test
- la probabilità pre-test viene rafforzata, o meno, da opportuni esami strumentali (test diagnostici) → probabilità post-test
Il rapporto di verosimiglianza di un test è un coefficiente che rappresenta quanto la probabilità pre-test di una malattia viene incrementata (o decrementata) in seguito all’esito del test, e consente dunque, tramite opportuni passaggi, di determinare la probabilità post-test.
Ricordiamo a questo punto che la sensibilità e la specificità di un test diagnostico sono caratteristiche intrinseche relative alla sua affidabilità e non hanno nulla a che vedere con la probabilità che un paziente abbia, o meno, una certa malattia.
Il valore predittivo di un test invece può essere interpretato come caso particolare di probabilità post-test in cui la probabilità pre-test corrisponde alla prevalenza della malattia. Infatti il procedimento che abbiamo utilizzato per calcolare il valore predittivo è il medesimo che vedremo tra poco, applicando di nuovo il teorema di Bayes.
DEFINIZIONE DI RAPPORTO DI VEROSIMIGLIANZA (LIKELIHOOD RATIO)
Il rapporto di verosimiglianza LR di un test è il rapporto tra la probabilità che il test abbia un certo esito in un paziente malato e la probabilità che il test dia lo stesso esito in un paziente sano.
\ LR =\large \frac{probabilità \, che \, il \, test\, abbia\, un \,certo \, esito\, in \, un\, paziente \, malato}{probabilità \, che \, il \, test\, abbia\, lo\,stesso\, esito\, in \, un\, paziente \, sano}
A seconda che l’esito del test sia positivo o negativo possiamo definire il rapporto di verosimiglianza positivo LR+ (positive likelihood ratio) e il rapporto di verosimiglianza negativo LR- (negative likelihood ratio).
Il rapporto di verosimiglianza positivo è il rapporto tra la probabilità di avere un vero positivo (sensibilità) e la probabilità di avere un falso positivo (1-specificità). Il rapporto di verosimiglianza negativo è invece il rapporto tra la probabilità di avere un falso negativo (1-sensibilità) e la probabilità di avere un vero negativo (specificità).
\small LR+ =\large \frac{sens}{1-spec}
\small LR- =\large \frac{1-sens}{spec}
Per trovare l’odds post-test si può utilizzare la seguente relazione, che deriva da un’applicazione diretta del teorema di Bayes:
\small odds\,posttest = LR \cdot odds\,pretest
In generale, ricordiamo la relazione che lega l’odds con la probabilità (che abbiamo già trovato parlando di rischio relativo e odds ratio): \small odds =\large \frac{prob}{1-prob}, da cui \small prob =\large \frac{odds}{1+odds}
In caso di test in sequenza, l’odds post-test può essere determinato nel seguente modo, a patto che i test eseguiti siano indipendenti:
\small odds\,posttest = LR1 \cdot LR2 \cdot LR3 \cdot odds\,pretest
LIKELIHOOD RATIO E TEOREMA DI BAYES
La formula per il calcolo dell’odds post-test deriva da un’applicazione diretta del teorema di Bayes.
Indicando con P(M|+) la probabilità post-test, con P(M) la probabilità pre-test, con P(+|M) la sensibilità e con P(+|S) 1 – specificità, troviamo:
\small prob\,posttest = P(M|+) =\large \frac{P(+|M)\cdot P(M)}{P(+|M)\cdot P(M) + P(+|S)\cdot (1-P(M))}=\frac{sens\cdot prob\,pretest}{sens\cdot prob\,pretest + (1-spec)\cdot (1-prob\,pretest)}
Quindi, per trovare l’odds post-test:
\small odds\,posttest \large=\frac{prob\,posttest}{1-prob\,posttest}\small=\large\frac{sens\cdot prob\,pretest}{sens\cdot prob\,pretest + (1-spec)\cdot(1- prob\,pretest)}\small:(1-\large \frac{sens\cdot prob\,pretest}{sens\cdot prob\,pretest + (1-spec)\cdot(1- prob\,pretest)})\small=\large\frac{sens\cdot prob\,pretest}{sens\cdot prob\,pretest + (1-spec)\cdot (1-prob\,pretest)}\small\cdot \large\frac{sens\cdot prob\,pretest + (1-spec)\cdot (1-prob\,pretest)-sens\cdot prob\,pretest}{sens\cdot prob\,pretest + (1-spec)\cdot (1-prob\,pretest)}\small=\large\frac{sens\cdot prob\,pretest}{sens\cdot prob\,pretest + (1-spec)\cdot (1-prob\,pretest)}\small\cdot\large\frac{sens\cdot prob\,pretest + (1-spec)\cdot(1- prob\,pretest)}{(1-spec)\cdot (1-prob\,pretest)}\small=\large\frac{sens}{1-spec}\small\cdot\large\frac{ prob\,pretest}{1-prob\,pretest} \small = \\ LR \cdot odds\,pretest
ESERCIZIO SUL RAPPORTO DI VEROSIMIGLIANZA (LIKELIHOOD RATIO)
Supponiamo che un paziente si rechi dal medico lamentando forti dolori addominali. Sulla base dei segni e dei sintomi, il medico stima che la probabilità che il paziente abbia un’appendicite è pari al 40% e decide di effettuare una radiografia per affinare la diagnosi, che dà esito positivo. Se la sensibilità della radiografia per la diagnosi di appendicite è dell’90% e la specificità è del 70%, qual è la probabilità a posteriori che il paziente abbia l’appendicite?
Disclaimer: i dati sono ipotetici.
Siccome il test ha dato esito positivo, calcoliamo il rapporto di verosimiglianza positivo (positive likelihood ratio) della radiografia: \small LR+ =\large \frac{sens}{1-spec} \small= \large\frac{0,90}{1-0,70}\small= \large\frac{0,90}{0,30} \small= 3,0
Siccome conosciamo la probabilità pre test, dobbiamo convertire questa probabilità in odds pre test: \small odds\,pretest=\large\frac{prob\,pretest}{1-prob\,pretest}\small=\large\frac{0,40}{1-0,40}\small=0,67
Calcoliamo ora l’odds post test: \small odds\,posttest = LR \cdot odds\,pretest = 3,0\cdot 0,67=2,01
Covertiamo l’odds posttest in probabilità post test: \small prob\,posttest=\large\frac{odds\,posttest}{1+odds\,posttest}\small=\large\frac{2,01}{1+2,01}\small=0,67
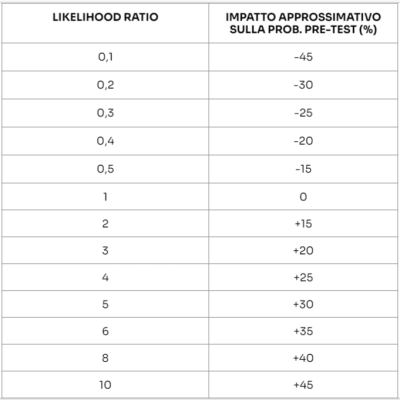
IMPATTO DEL LIKELIHOOD RATIO SULLA PROBABILITÀ PRE-TEST
- Se 0 < LR < 1 allora la probabilità post-test diminuisce. I valori più vicini a zero hanno un impatto maggiore dei valori vicini a 1.
- LR = 1 non ha alcun impatto sulla probabilità post-test.
- Se LR > 1 la probabilità post-test aumenta.
Con l’esempio sopra abbiamo notato che calcolare la probabilità post-test sia piuttosto laborioso, siccome bisogna convertire varie volte gli odds in probabilità e le probabilità in odds.
Lasciamo quindi una tabella riassuntiva sull’impatto approssimativo del likelihood ratio (1).
NOMOGRAMMA DI FAGAN E PROBABILITÀ POST-TEST
Un metodo alternativo per il calcolo della probabilità post-test proposto dal Dottor Terrence J. Fagan, che si trova in una lettera scritta al New England Journal of Medicine del 1975, prevede l’utilizzo di un nomogramma, e permette di calcolare la probabilità post-test in modo rapido, anche se approssimativo.
L’immagine del nomogramma è presa dall’articolo originale (2).
Il procedimento per determinare la probabilità post-test con il nomogramma di Fagan è molto semplice, e funziona come segue.
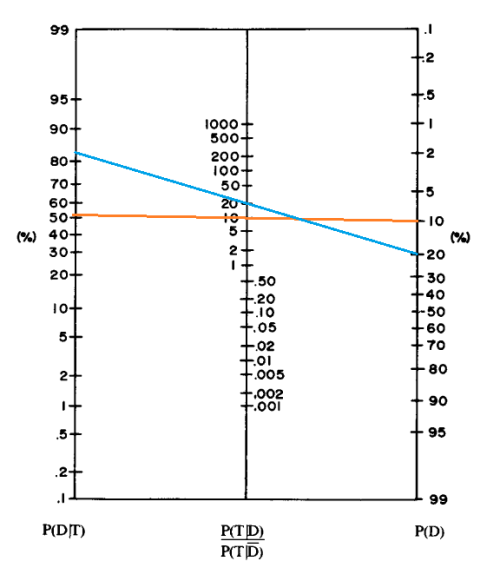
A sinistra del nomogramma troviamo la probabilità post test P(D|T), dove D sta per Disease, al centro il rapporto di verosimiglianza, espresso in termini di probabilità condizionata, e a destra troviamo la probabilità pre-test.
Per determinare la probabilità post-test si traccia una linea che interseca i valori della probabilità pre-test e del rapporto di verosimiglianza (che sono noti) e la si prolunga fino a intersecare il righello a sinistra.
Ad esempio, la linea arancione illustra il caso in cui si ha una probabilità pre-test del 10% e un LR pari a 10. La probabilità post-test in questo caso è superiore al 50%.
La linea azzurra invece è il caso in cui si ha una probabilità pre-test del 20% e un LR pari a 20. La probabilità post-test risulta superiore all’80%
Fonti e note:
- (1) McGee S. Simplifying likelihood ratios. J Gen Intern Med. 2002;17(8):646-649.
- (2) Fagan TJ. Nomogram for Bayes’s theorem. N Engl J Med. 1975; 293: 257
- (3) Hayden SR, Brown MD: Likelihood ratio: A powerful tool for incorporating the results of a diagnostic test into clinical decisionmaking. Ann Emerg Med May 1999;33:575-580.

