Sensibilità e Specificità di un Test Diagnostico
SENSIBILITÀ E SPECIFICITÀ DI UN TEST DIAGNOSTICO

La sensibilità e la specificità sono due indicatori fondamentali per poter interpretare correttamente il risultato di un test diagnostico.
Dopo una breve introduzione di contestualizzazione, vediamo come si definiscono e come è possibile calcolarli a partire dalla tabella di errata classificazione.
PREMESSA. A COSA SERVONO I TEST DIAGNOSTICI
Con il termine test diagnostico si indica una grande famiglia di esami il cui scopo è determinare la probabilità che un individuo abbia, o meno, una certa patologia.
Alcuni esempi di test possono essere i test di screening (Pap test, mammografia per il tumore al seno, ecc.) gli esami di laboratorio (misurazione della glicemia, dosaggio TSH, dosaggio PSA, ecc.) o gli esami diagnostici per immagini (Risonanza magnetica, TAC, Radiografia, ecc.).
Come possiamo immaginare, nessun test determina in modo inequivocabile la presenza di una certa malattia.
CUT-OFF DI UN TEST DIAGNOSTICO. ALCUNE CONSIDERAZIONI
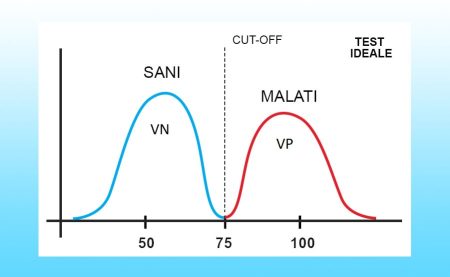
Supponiamo di voler determinare se un paziente abbia una certa malattia X sottoponendolo a un test che riesca a valutare la concentrazione nel sangue di un certo elemento Y (1). Ebbene, nella situazione ideale potremmo determinare un valore di cut-off (valore soglia) del test diagnostico in cui tutti gli individui sani si distribuiscono attorno a certi valori di concentrazione dell’elemento Y, inferiori al cut-off, e tutti gli individui malati si concentrano attorno a valori maggiori del cut-off. Diremo che il paziente risulta positivo al test se il test dà un valore maggiore al cut-off, e risulta negativo nel caso opposto.
Nella situazione ideale i pazienti sono tutti classificati correttamente, ovvero tutti i malati sono veri positivi VP, e tutti i sani sono veri negativi VN. Non abbiamo quindi né falsi positivi FP (pazienti in realtà sani ma che risultano positivi al test), né falsi negativi FN (pazienti malati che risultano negativi al test).
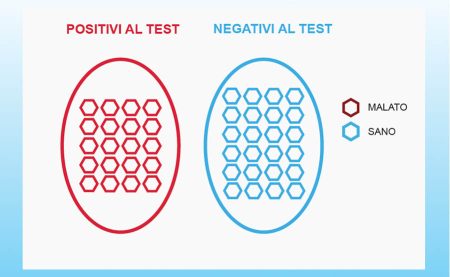
Per fare un esempio, dopo aver scelto un opportuno valore di cut-off, supponiamo di sottoporre 44 persone a un test, di cui 20 sono malate e 24 sane. Il test ideale le classifica tutte correttamente, come rappresentato di seguito:
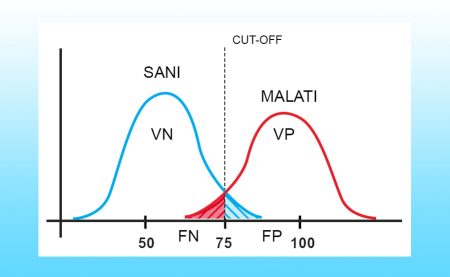
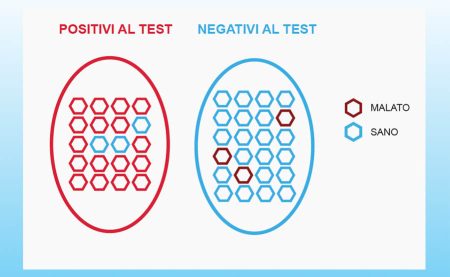
Una rappresentazione più verosimile della realtà è invece la seguente, dove possiamo avere pazienti sani in cui il test dà un valore maggiore del cut-off scelto, e vengono classificati falsamente come positivi FP, e pazienti malati in cui il test dà un valore maggiore del cut-off, classificati dunque falsamente come negativi FN.
Si può subito notare che scegliendo un valore di cut-off maggiore, quindi spostando a destra la linea tratteggiata, si avranno meno falsi positivi. Viceversa, scegliendo un cut-off minore, spostando la linea a sinistra, si otterranno meno falsi negativi.
SIGNIFICATO DI AFFIDABILITÀ DI UN TEST DIAGNOSTICO
Supponiamo ora di avere a disposizione un test diagnostico per una certa malattia. Come possiamo capire se il test è accurato oppure no? Una possibile modalità di validazione del test è quella di fare uno studio statistico conoscendo a priori la corretta classificazione del gruppo di pazienti che sottoporremo al test. In altre parole, dato un gruppo di pazienti, dovremmo conoscere a priori quanti sono malati e quanti sono sani, sottoporli al test, e contare quanti vengono correttamente individuati. In sostanza, il test dovrebbe essere comparato con un altro metodo di classificazione, assunto come riferimento, che viene chiamato gold standard.
Uno studio statistico per la validazione di un test è basato sulla tabella di errata classificazione (o matrice di confusione) che contiene il numero di casi classificati correttamente o falsamente.

Sulla diagonale principale abbiamo due classificazioni corrette: veri positivi VP e veri negativi VN. Sulla diagonale secondaria abbiamo invece due classificazioni non corrette: falsi positivi FP e falsi negativi FN. Il totale dei malati si trova sommando veri positivi VP con falsi negativi FN, mentre il totale dei malati si trova sommano falsi positivi FP con veri negativi VN.
Il test perfetto non dovrebbe produrre né falsi positivi né falsi negativi.
Una possibile misura dell’affidabilità di un test diagnostico è l’accuratezza, che misura la percentuale di diagnosi corrette, ovvero quanti pazienti vengono classificati correttamente.
ACCURATEZZA = (VP+VN)/TOT PAZIENTI
Facciamo ora un esempio. Supponiamo di avere 102 pazienti, di cui conosciamo a priori la corretta classificazione, e di sottoporli a un certo test diagnostico. La tabella di errata classificazione è la seguente, dove abbiamo 48 + 38 = 86 persone classificate correttamente, e 6 + 10 = 16 persone classificate falsamente.

Di seguito un’esemplificazione grafica dell’esperimento:

LA DEFINIZIONE DI SENSIBILITÀ DI UN TEST DIAGNOSTICO

La sensibilità di un test diagnostico è la proporzione di malati che vengono classificati in maniera corretta, ed è dunque l’indicatore che ci permette di rispondere alla domanda: se un individuo è malato, qual è la probabilità che il test diagnostico dia risultato positivo?
SENSIBILITÀ = VERI POSITIVI/TOT MALATI
Un test altamente sensibile è preferibile se l’obiettivo è quello di individuare il maggior numero di malati, come nel caso dei test di screening, perché dà meno risultati falsi negativi.
Un test è sensibile al 100% quando tutti i malati risultano positivi, quindi nessun malato sfuggirà al test.
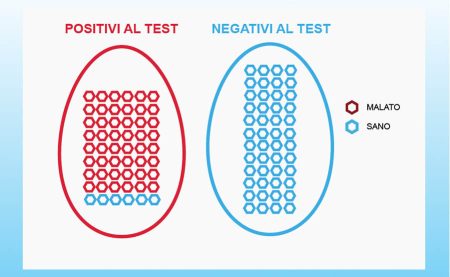
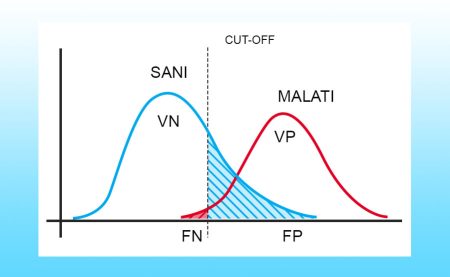
Prendiamo ora in considerazione la tabella dell’esempio sopra e calcoliamo la sensibilità del test.
Siccome il totale dei malati si trova sommando veri positivi e falsi negativi (TOT MALATI = VP + FN = 48 + 10 = 58), la sensibilità di questo test sarà SENS=VP/TOT MALATI=48/58=83%. Ovvero, se sottoponiamo a questo test 100 malati, 17 di essi sfuggiranno al test.
LA DEFINIZIONE DI SPECIFICITÀ DI UN TEST DIAGNOSTICO

La specificità di un test diagnostico è la proporzione di sani classificati correttamente. In altri termini, la specificità è la probabilità che un individuo sano risulti negativo al test.
SPECIFICITÀ = VERI NEGATIVI/TOT SANI
Un test altamente specifico dà meno falsi positivi, quindi è ottimo per accertarsi della presenza di una patologia.
Un test è specifico al 100% quando tutti i sani risultano negativi, quindi nessun paziente sano avrà una diagnosi errata.
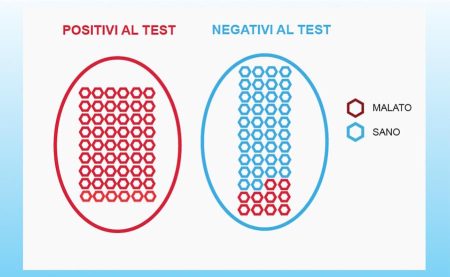
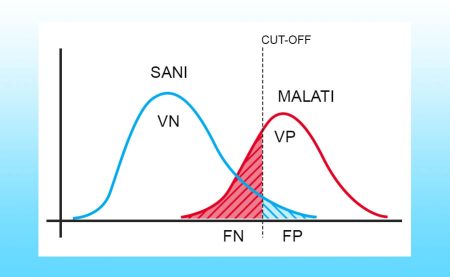
Calcoliamo ora la specificità dell’esempio sopra. Il totale dei pazienti malati si trova sommando veri negativi con falsi positivi (TOT SANI = VN + FP = 38 + 6 = 44), dunque la specificità di questo test sarà: SPEC = VN/TOT SANI = 38/44 = 86%. Quindi, se sottoponiamo al test 100 pazienti sani, 14 di essi avranno una diagnosi errata, ovvero risulteranno positivi al test nonostante non siano effettivamente malati.
Per riassumere:

Generalmente è difficile ottenere un test che sia altamente specifico e al contempo sensibile: rendere un test più specifico può renderlo meno sensibile, e viceversa. Esiste a questo proposito uno strumento che mette in relazione sensibilità e specificità di un test, permette di fare valutazioni riguardanti le sue performance e consente di determinare il migliore valore di cut-off: la curva ROC (Receiver Operating Characteristic), su cui abbiamo scritto un articolo dedicato.
Sottolineiamo che la sensibilità e la specificità di un test non permetto di rispondere alla domanda: se un paziente risulta positivo a un test, qual è la probabilità che egli sia effettivamente malato?
Per poter rispondere a questa domanda è necessario introdurre il concetto di VALORE PREDITTIVO e di RAPPORTO DI VEROSIMIGLIANZA (LIKELIHOOD RATIO).
Se si volesse invece determinare la probabilità di contrarre una certa malattia in caso di esposizione a determinati fattori di rischio è necessario introdurre i concetti di rischio relativo e odds ratio.
Per un ulteriore approfondimento con cenni elementari di calcolo di probabilità rimandiamo all’articolo: Affidabilità di un test diagnostico: matematica e teorema di Bayes
ESERCIZI SU SPECIFICITÀ E SENSIBILITÀ
Per alcuni esercizi svolti sulla sensibilità, la specificità e il valore predittivo dei test diagnostici rimandiamo alla pagina: Esercizi sui test diagnostici: sensibilità, specificità, valore predittivo, curva ROC.
Fonti e note:
- (1) Non per tutti i test diagnostici si possono determinare valori di cut-off. Altri test che si basano, ad esempio, sulla presenza, o meno, di alterazioni citologiche danno chiaramente un risultato dicotomico.
- Biostatistica, Marcello Pagano, Kimberlee Gauvreau
- Introductory Biostatistics, 2nd Edition, Chap T. Le, Lynn E. Eberly

